Bellman-Ford Algorithm

Bellman-Ford 演算法是一種用於解決最短路徑問題的演算法，可以處理包含負權重邊的圖。

演算法

1. 初始化：首先，將所有節點的距離值設置為無限大（或一個足夠大的數），並將起始節點的距離值設置為零。
2. 遍歷邊：然後，重複遍歷所有的邊，每次遍歷時，檢查從源節點到目標節點的路徑是否比目前已知的最短路徑更短。如果是，則更新目標節點的距離值為新的最短距離。
3. 重複：重複執行上述步驟 次，其中 是圖中節點的總數。這是因為在最壞情況下，最短路徑不會比圖中的節點數多一個還要長。
4. 檢查負權環：最後，再次遍歷所有的邊，如果仍然可以找到更短的路徑，這意味著圖中存在一個負權環。Bellman-Ford 演算法可以用來偵測負權環的存在。

Bellman-Ford 演算法通過不斷嘗試更新節點之間的最短距離，來找到從一個指定的源節點到圖中所有其他節點的最短路徑。

如果存在負權環，則演算法會檢測到它們。這個演算法的時間複雜度為 ，其中 是節點數， 是邊數。

// Bellman Ford Algorithm in Kotlin

class BellmanFord {

    fun bellmanFord(graph: Array<IntArray>, V: Int, E: Int, src: Int) {
        // Initialize distance of all vertices as infinite.
        val dis = IntArray(V)
        for (i in 0 until V) dis[i] = Int.MAX_VALUE

        // initialize distance of source as 0
        dis[src] = 0

        // Relax all edges |V| - 1 times. A simple shortest
        // path from src to any other vertex can have at-most |V| - 1 edges
        for (i in 0 until V - 1) {
            for (j in 0 until E) {
                if (dis[graph[j][0]] != Int.MAX_VALUE && dis[graph[j][0]] + graph[j][2] < dis[graph[j][1]])
                    dis[graph[j][1]] = dis[graph[j][0]] + graph[j][2]
            }
        }

        // check for negative-weight cycles.
        for (i in 0 until E) {
            val x = graph[i][0]
            val y = graph[i][1]
            val weight = graph[i][2]
            if (dis[x] != Int.MAX_VALUE && dis[x] + weight < dis[y])
                println("Graph contains negative weight cycle")
        }

        println("Vertex Distance from Source")
        for (i in 0 until V) println("$i\t\t${dis[i]}")
    }
}

// main function
fun main(args: Array<String>) {
    val V = 5 // Number of vertices in graph
    val E = 8 // Number of edges in graph

    // Every edge has three values (u, v, w) where
    // the edge is from vertex u to v. And weight
    // of the edge is w.
    val graph = arrayOf(
        intArrayOf(0, 1, -1),
        intArrayOf(0, 2, 4),
        intArrayOf(1, 2, 3),
        intArrayOf(1, 3, 2),
        intArrayOf(1, 4, 2),
        intArrayOf(3, 2, 5),
        intArrayOf(3, 1, 1),
        intArrayOf(4, 3, -3)
    )

    val bellmanFord = BellmanFord()
    bellmanFord.bellmanFord(graph, V, E, 0)
}

Floyd-Warshall Algorithm

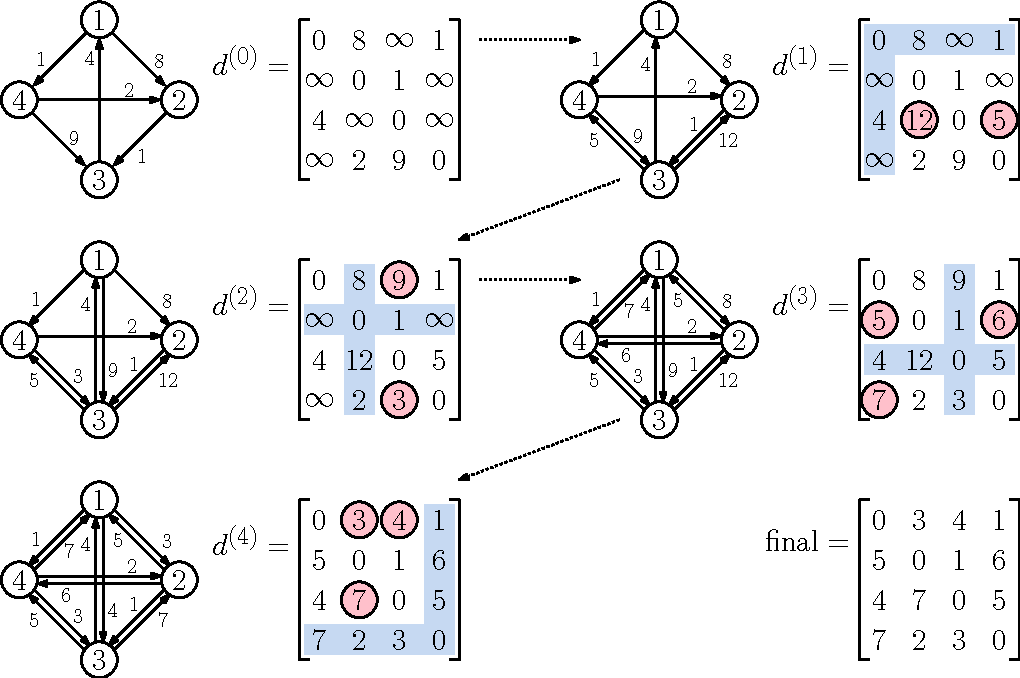
Floyd-Warshall 演算法是一種用於解決所有節點對之間最短路徑問題的演算法。

它適用於有向圖或帶權有向圖，其中每條邊都有一個非負權重。

演算法

1. 初始化：創建一個二維陣列（矩陣），稱為距離矩陣，其大小為節點數。將距離矩陣的對角線設置為0，表示每個節點到自己的距離為0。將其他未直接相連的節點之間的距離設置為無窮大或一個足夠大的值。
2. 迭代計算最短路徑：對於每一對節點（i和j），以及每一個中間節點k，計算從節點i到節點j經過節點k的距離是否比直接從i到j的距離短。如果是的話，則更新距離矩陣中i到j的距離為更小的值。
3. 重複迭代：重複步驟2，直到所有可能的節點對的最短路徑都被計算出來為止。這樣，距離矩陣中的值將包含所有節點對之間的最短路徑。
4. 結果：最後的距離矩陣將包含所有節點對之間的最短路徑距離。

Floyd-Warshall 演算法的時間複雜度是，其中是節點的數量。

優點是它可以處理包含負權邊的圖，並且它能夠找到所有節點對之間的最短路徑，而不僅僅是一對節點之間的最短路徑。

然而，對於大型圖，它的運行時間可能會變得很長。

// Floyd-Warshall Algorithm in Kotlin

// INF 
val INF = 99999

class FloydWarshall {

    // Number of vertices in the graph
    private val V = 4

    // Define infinity as the large enough value. This value will be
    // used for vertices not connected to each other
    private val INF = 99999

    // Solves the all-pairs shortest path problem using Floyd Warshall algorithm
    fun floydWarshall(graph: Array<IntArray>) {
        /* dist[][] will be the output matrix that will finally
        have the shortest distances between every pair of vertices */
        val dist = Array(V) { IntArray(V) }
        var i: Int
        var j: Int
        var k: Int

        /* Initialize the solution matrix same as input graph matrix.
        Or we can say the initial values of shortest distances
        are based on shortest paths considering no intermediate
        vertex. */
        i = 0
        while (i < V) {
            j = 0
            while (j < V) {
                dist[i][j] = graph[i][j]
                j++
            }
            i++
        }

        /* Add all vertices one by one to the set of intermediate
        vertices.
        ---> Before start of an iteration, we have shortest
        distances between all pairs of vertices such that
        the shortest distances consider only the vertices in
        set {0, 1, 2, .. k-1} as intermediate vertices.
        ----> After the end of an iteration, vertex no. k is
        added to the set of intermediate vertices and the
        set becomes {0, 1, 2, .. k} */
        k = 0
        while (k < V) {
            // Pick all vertices as source one by one
            i = 0
            while (i < V) {
                // Pick all vertices as destination for the
                // above picked source
                j = 0
                while (j < V) {
                    // If vertex k is on the shortest path from
                    // i to j, then update the value of dist[i][j]
                    if (dist[i][k] + dist[k][j] < dist[i][j])
                        dist[i][j] = dist[i][k] + dist[k][j]
                    j++
                }
                i++
            }
            k++
        }

        // Print the shortest distance matrix
        printSolution(dist)
    }

    /* A utility function to print solution */
    fun printSolution(dist: Array<IntArray>) {
        println("The following matrix shows the shortest " + "distances between every pair of vertices")
        var i = 0
        while (i < V) {
            var j = 0
            while (j < V) {
                if (dist[i][j] == INF)
                    print("%7s".format("INF"))
                else
                    print("%7d".format(dist[i][j]))
                j++
            }
            println()
            i++
        }
    }
}

// main function
fun main(args: Array<String>) {
    /* Let us create the following weighted graph
            10
    (0)------->(3)
        |     /|\
    5 |     |
        |     | 1
    \|/     |
    (1)------->(2)
            3     */
    val graph = arrayOf(intArrayOf(0, 5, INF, 10),
            intArrayOf(INF, 0, 3, INF),
            intArrayOf(INF, INF, 0, 1),
            intArrayOf(INF, INF, INF, 0))
    val a = FloydWarshall()

    // Print the solution
    a.floydWarshall(graph)
}

所有 Code 可以在 Github 找到 ～

明天會接著介紹 Prim's Algorithm 和 Kruskal's Algorithm

Reference

• Bellman–Ford algorithm example
• All-Pairs Shortest Paths and the Floyd-Warshall Algorithm